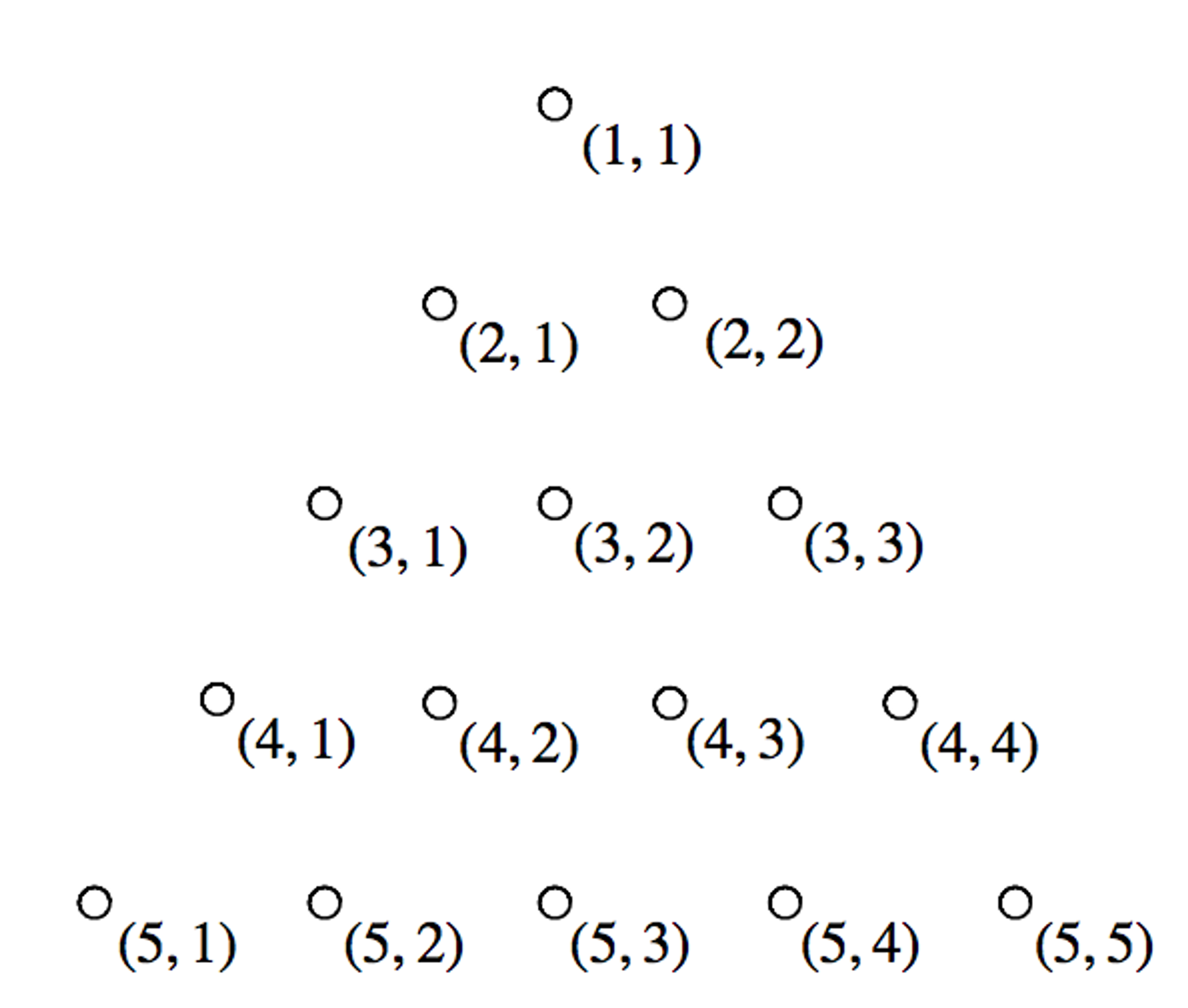imos법에 대해 알아보자.
Table of Contents
imos법 (いもす法, imos法)
개요
imos법은 다음과 같은 문제에서 쓸 수 있는 간단한 아이디어이다. (조금 더 formal한 설명을 할 수도 있지만, 예제만 봐도 충분히 이해할 수 있을 것이다.)
가게에 명의 손님이 방문한다. 가게는 시간 부터 까지 운영한다. 각각의 손님 에 대해 입장 시각 와 퇴장 시각 이 주어진다. 가게 운영 중 손님이 가장 많이 방문했을 때의 손님 수는 몇 명인가? (단, 동일 시각에 입장과 퇴장이 같이 발생한 경우, 퇴장이 먼저 이루어진다고 가정한다.)
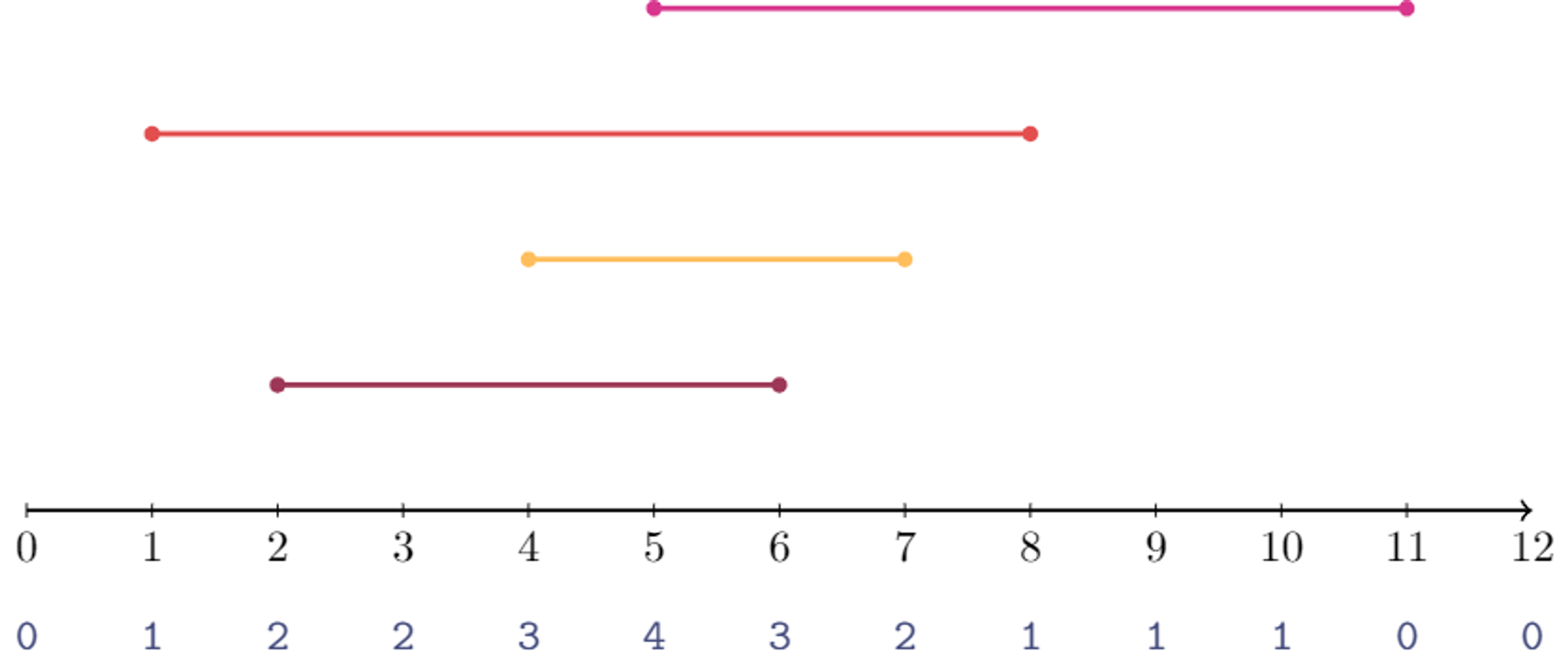
대충 저런 식의 쿼리 여러 개가 들어오는 모양새이다. 그림으로 나타낸다면, 수직선 위에 선을 여러 개 그어서, 가장 선이 많이 겹치는 부분을 구하는 것과 같다.
각 선분을 손님이 가게에 있던 시간으로 생각한다면, 시간 5에서 손님이 4명으로 가장 많다.
나이브하게 푼다면? 길이 짜리 배열 cnt을 초기화해두고, 각 손님마다 방문한 시간에 해당하는 배열값 cnt[s_i..e_i]에 모두 1을 더하는 방법을 생각해볼 수 있다. 그렇게 쿼리를 모두 처리하고 나면, cnt 배열의 최댓값이 답이 된다.
이렇게 하면, 쿼리 하나당 처리 시간이 이므로, 시간 복잡도는 가 된다. 더 빠르게 풀 수는 없을까?
입장과 퇴장만 기록
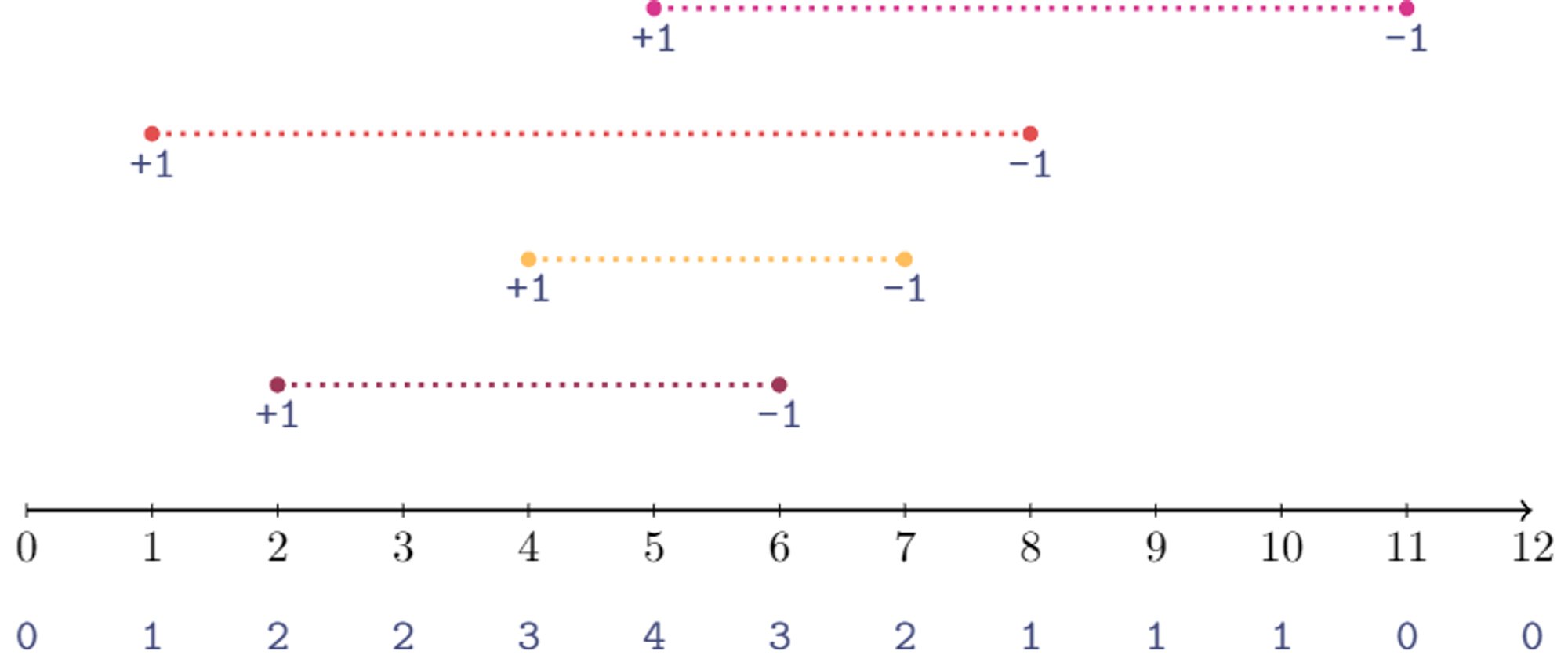
더 빠르게 풀 수 있다! imos법의 기본 아이디어는, "입장과 퇴장만 기록한다"로 요약할 수 있다. 말 그대로, 각 손님이 입장해서 퇴장하기까지 존재하는 모든 시각에 1을 더하는 것이 아니고, 입장할 때 +1을 기록하고, 퇴장할 때 -1을 기록해서, 모든 쿼리를 처리하고 나서 답을 구하기 전에 짜리 후처리 하나만 거치면 된다.
+1, -1만 기록해두고, 맨 마지막에 왼쪽부터 보면서 값을 시뮬레이팅한다.
결국 맨 마지막에 +1, -1이 기록된 배열의 누적합(Prefix sum) 배열을 구하면, 원래 우리가 구하려던 값이 나오는 것이다.
쿼리 하나당 두 값밖에 갱신하지 않으므로 쿼리당 처리 시간은 이고, 후처리는 이므로, 총 시간복잡도는 이다.
누적합과의 비교
어찌 보면 지금까지의 설명으로는 1차원 배열에서 쿼리를 처리하는 발상이라는 점에서 누적합과도 비슷해 보인다. Remind 차원에서 둘의 설명을 적어보았다.
•
누적합
◦
입력 다 받고, 전처리 한번 거치고 나면, 의 합을 구하는 것과 같은 쿼리를 빠르게 처리할 수 있다.
◦
쿼리 처리 도중 값 갱신이 일어나지 않는 경우에 사용한다.
•
imos법
◦
각 쿼리가 구간 내의 값을 갱신시키는 경우, 이를 매 쿼리마다 일일히 갱신하지 않고, 시작과 끝만 기록해두었다가 마지막에 한 번의 처리로 값을 시뮬레이팅하는 방법이다.
공식 레퍼런스와도 같은 いもす님의 블로그에서는 "imos법은 누적합 알고리즘을 다차원, 다차수로 확장시킨 것"이라고 설명되어 있다.
2차원에서의 imos법
격자 보드에 사각형 그리기
1차원 배열에서의 설명까지는 아마 많이들 알고 있을지도 모르겠다. 아니면 무의식 중에 그렇게 사용하고 있었거나... (나의 경우가 그렇다  )
)
하지만 imos법의 강력함은 이제부터이다. imos법은 특성상 고차원으로의 확장이 용이하다.
2차원 배열에서의 사용을 보이기 위해, 예시 문제를 보자. 이번에는 formal하게 작성해 보았다.
크기의 격자 보드가 있다. 각 칸의 초깃값은 모두 0이다.
다음과 같은 쿼리가 개 들어온다.
x1 y1 x2 y2 : , 에 해당하는 모든 칸 의 값에 1을 더한다.
쿼리를 모두 처리한 뒤의 최종 보드의 상태를 출력하라.
대충 감이 오는가? 그냥 1차원 배열에서 선분이 사각형으로 바뀌었을 뿐이다.
역시 나이브를 먼저 생각해본다면, 매 쿼리가 들어올 때마다 해당 사각형 영역에 1씩 직접 다 더해주고, 마지막에 출력만 해 주는 로직을 떠올려보자. 쿼리당 만큼 걸리고, 총 시간복잡도는 이다.
매 사각형(오렌지 영역)이 들어올 때마다 해당 영역의 모든 칸에 1씩 다 더해주면? 너무 느리다.
가로로 한번, 세로로 한번 휩쓸기
사각형으로 바뀌어도 기본적인 아이디어는 같다. "시작과 끝만 기록한다" 단 2차원에서는 차원이 늘어난 만큼, 가로 방향으로 시작과 끝, 세로 방향으로 시작과 끝 두 번 기록하고, 시뮬레이팅할 때도 가로로 한번, 세로로 한번 휩쓸면 된다. 갑자기 뭐 휩쓰는 얘기가 나오고 대체 무슨 소리냐?
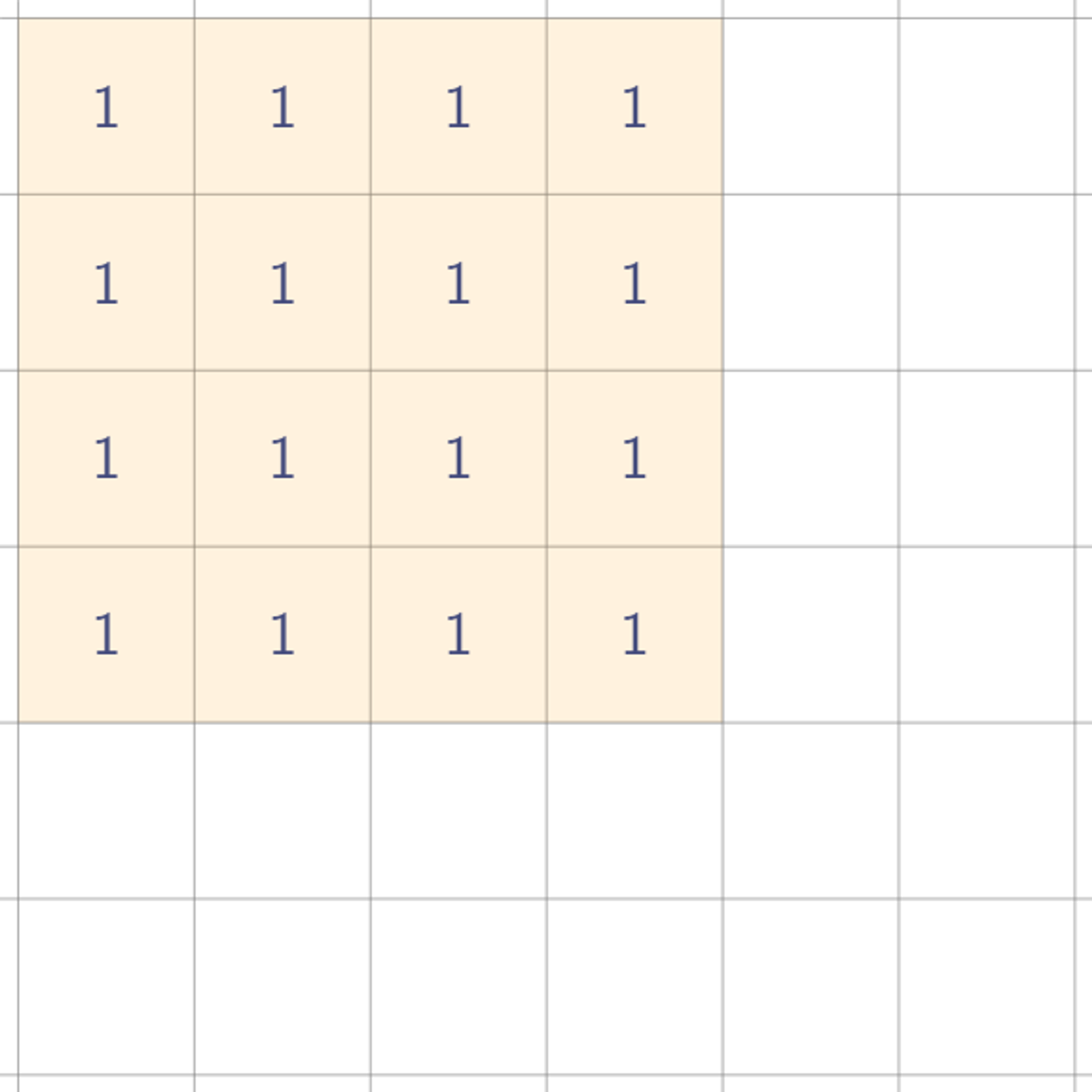
먼저 얘기하자면, 휩쓸으라는 얘기는 그냥 누적합을 구하라는 얘기다. 그래도 감이 안 잡힌다면, 그림으로 된 설명을 보자. 사각형 하나를 예로 들어보자.
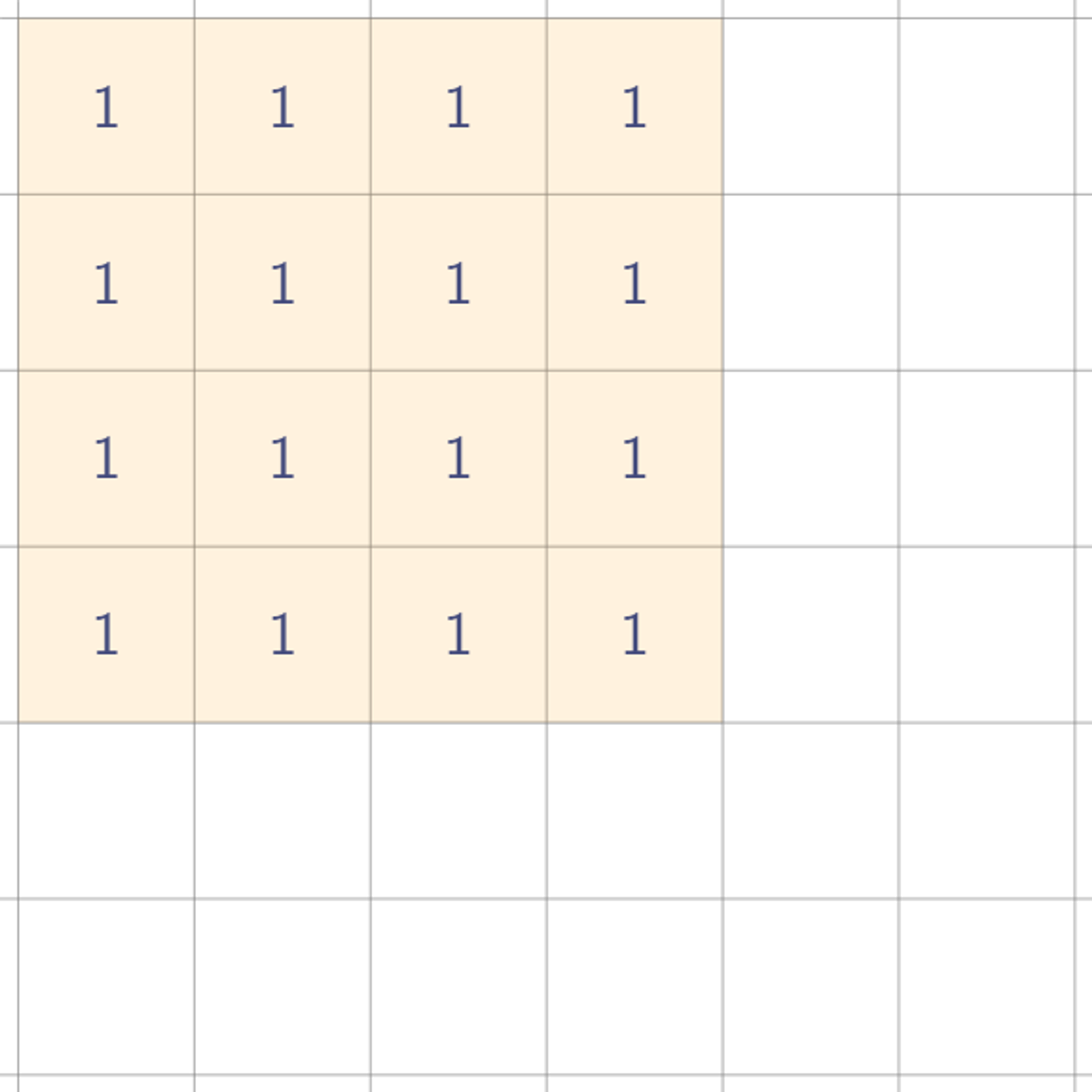
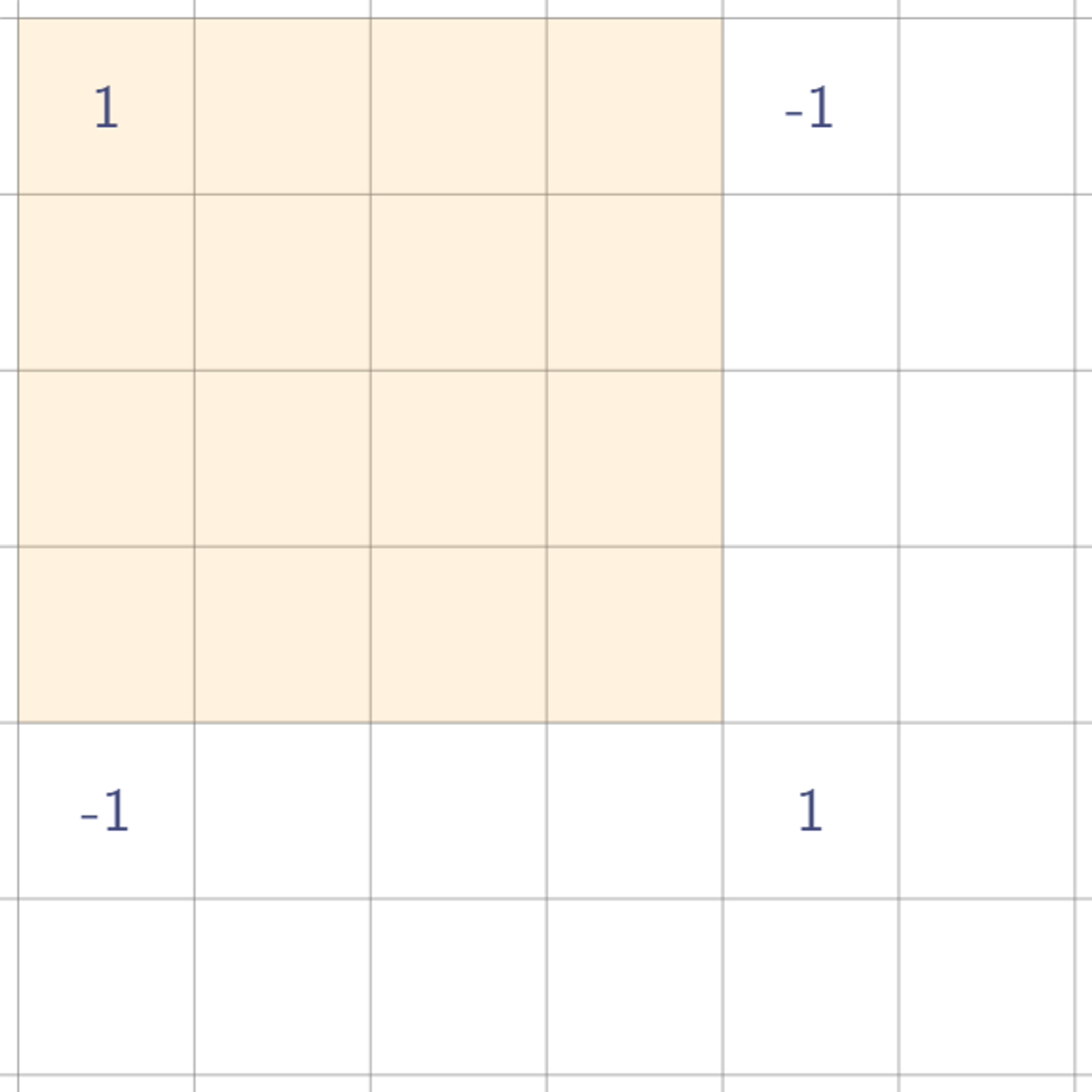
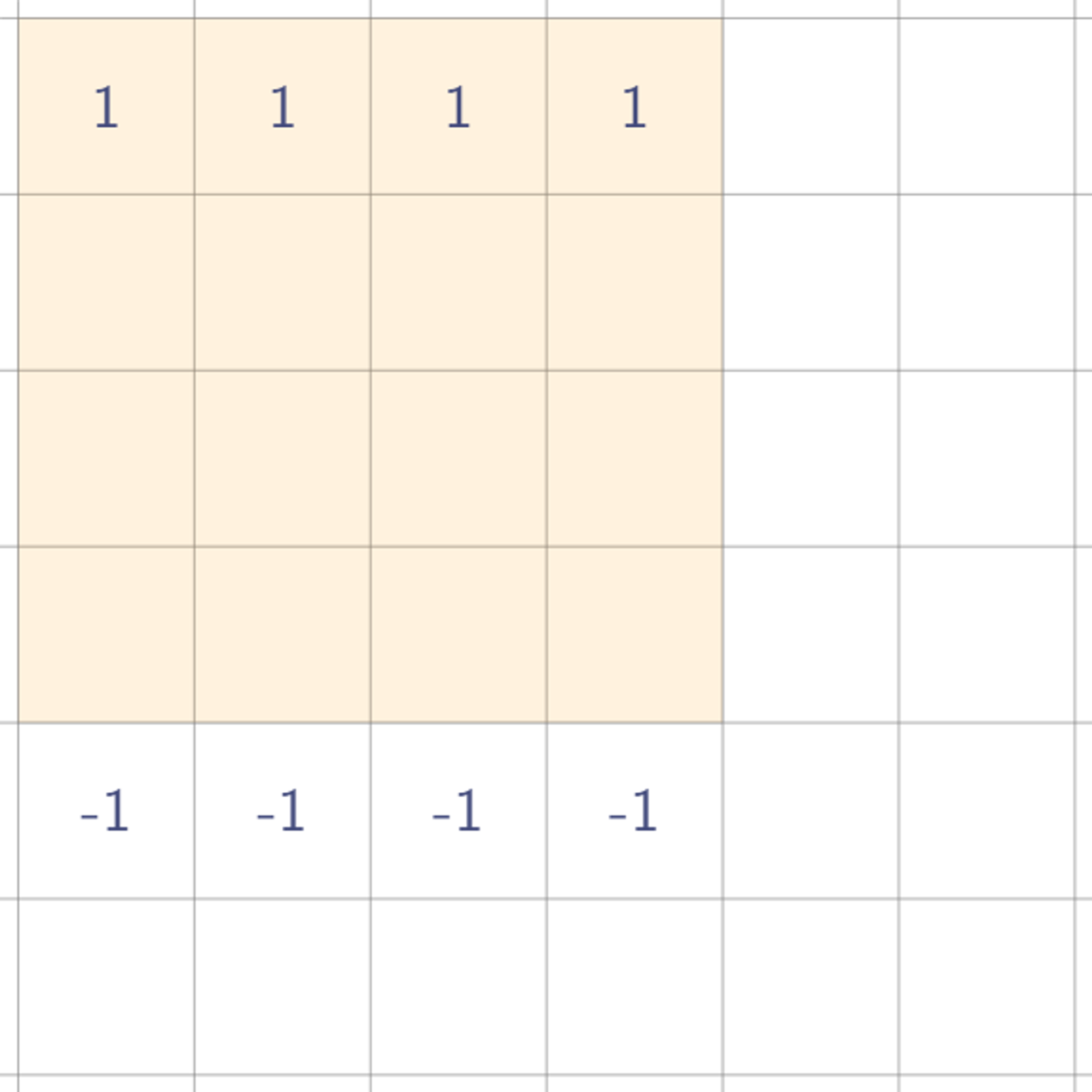
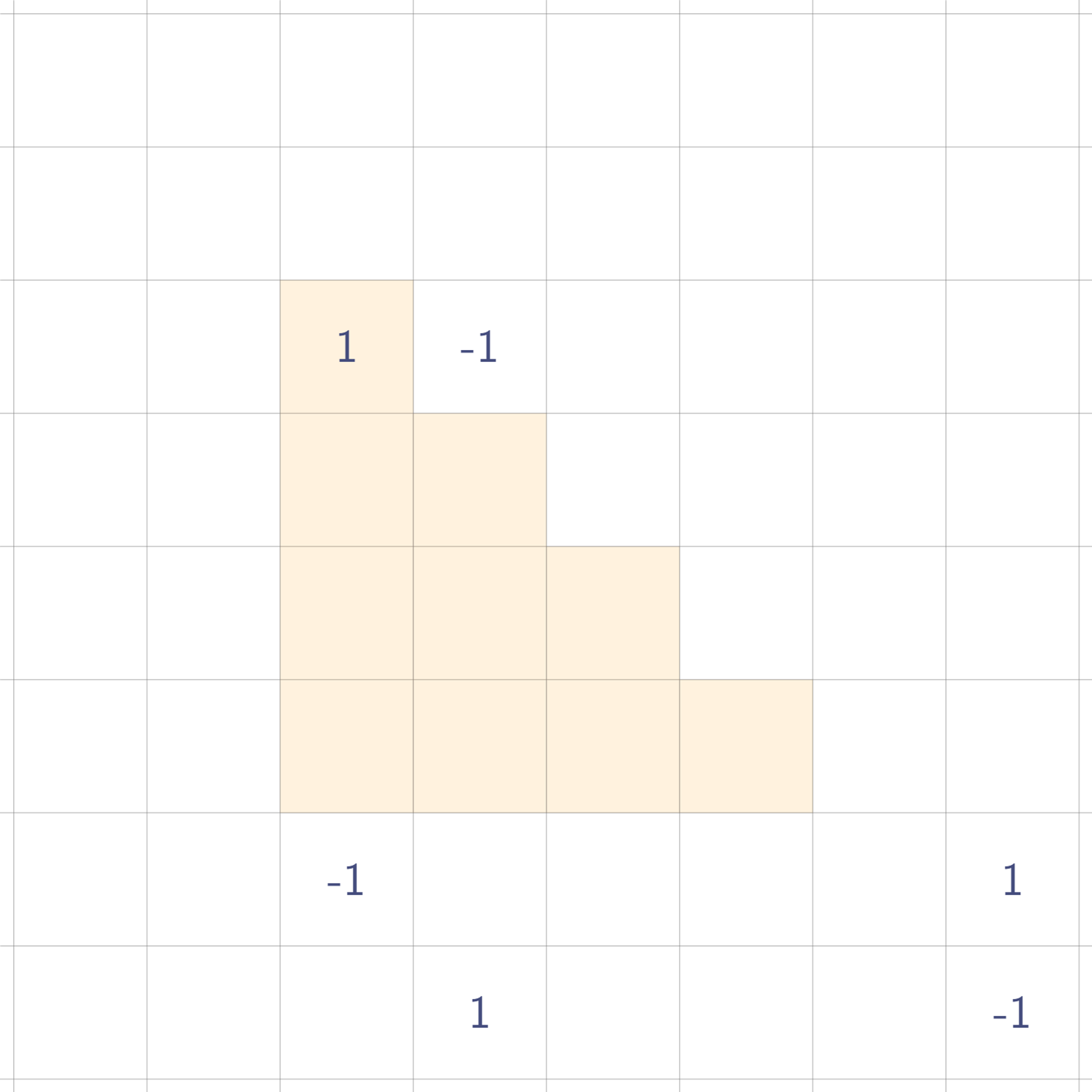
가로로 한번 휩쓸고, 세로로 한번 휩쓸어서 우리가 원하는 사각형 값이 나오게 하려면 값을 어떻게 찍어둬야 할까?
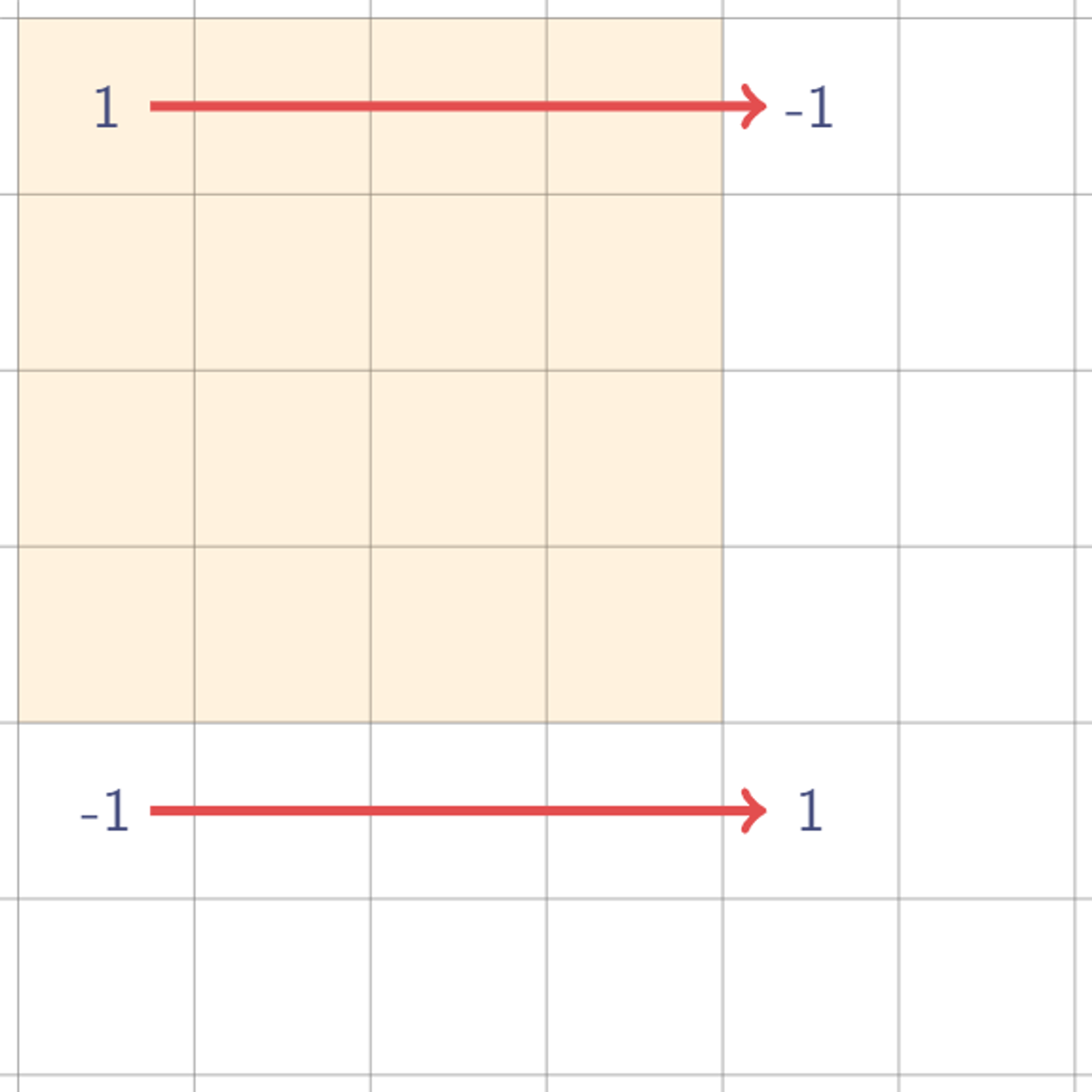
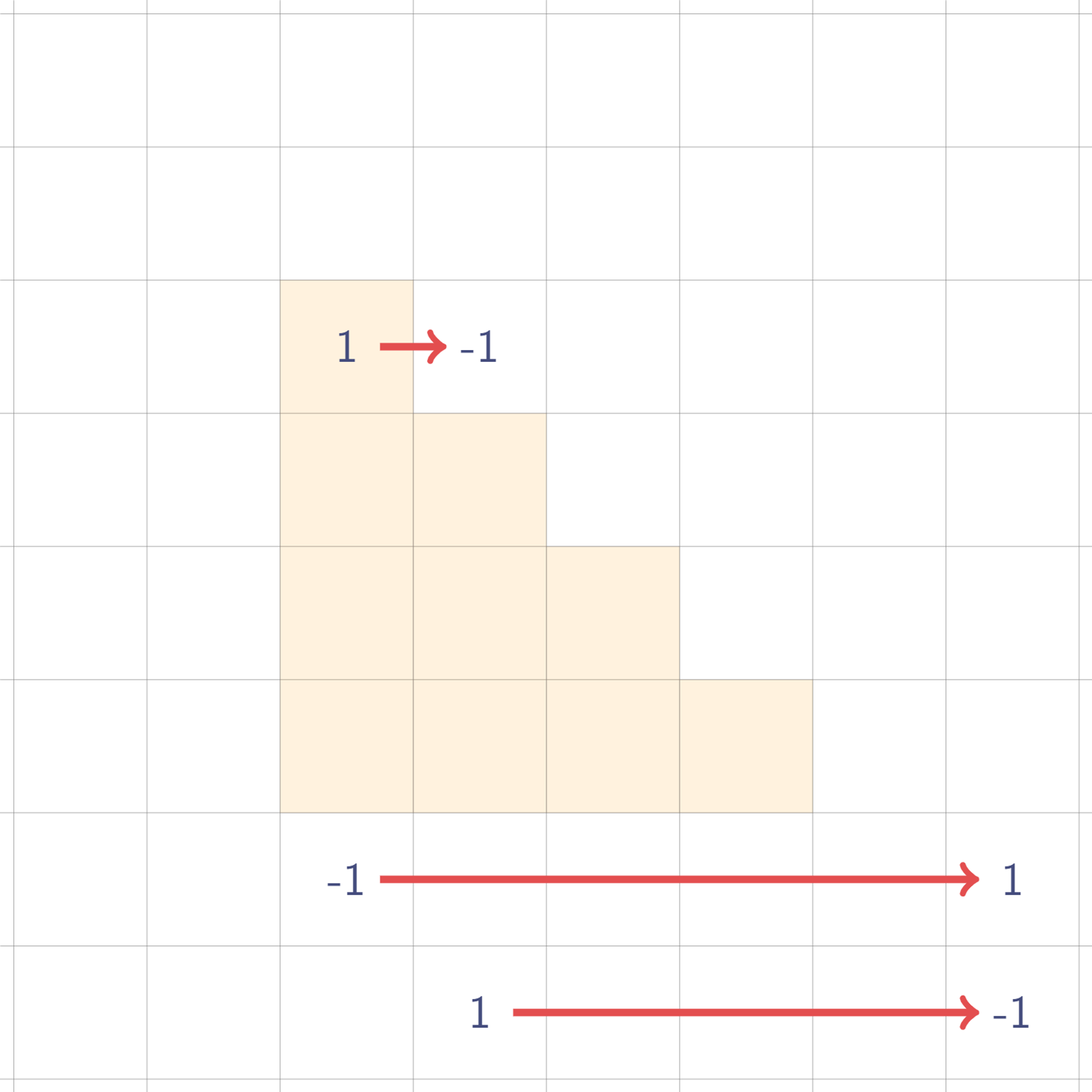
결론부터 말하면, 저렇게 값 네 개를 찍어두기만 하면, 원래 사각형 값을 시뮬레이팅할 수 있다. 실제로 저 네 개의 값을 찍어둔 채로 한번 휩쓸어보자. 우선 가로 방향으로 휩쓸면?
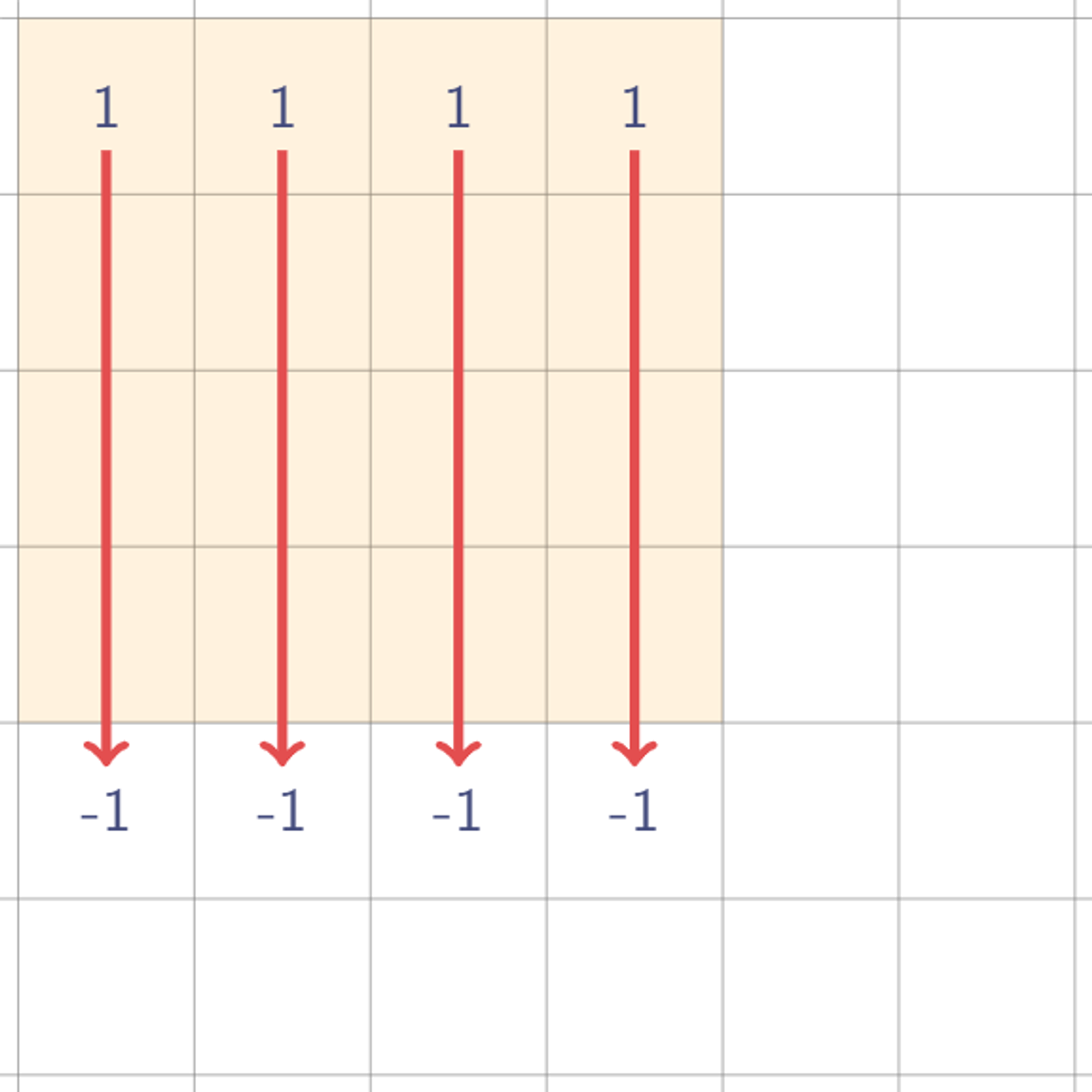
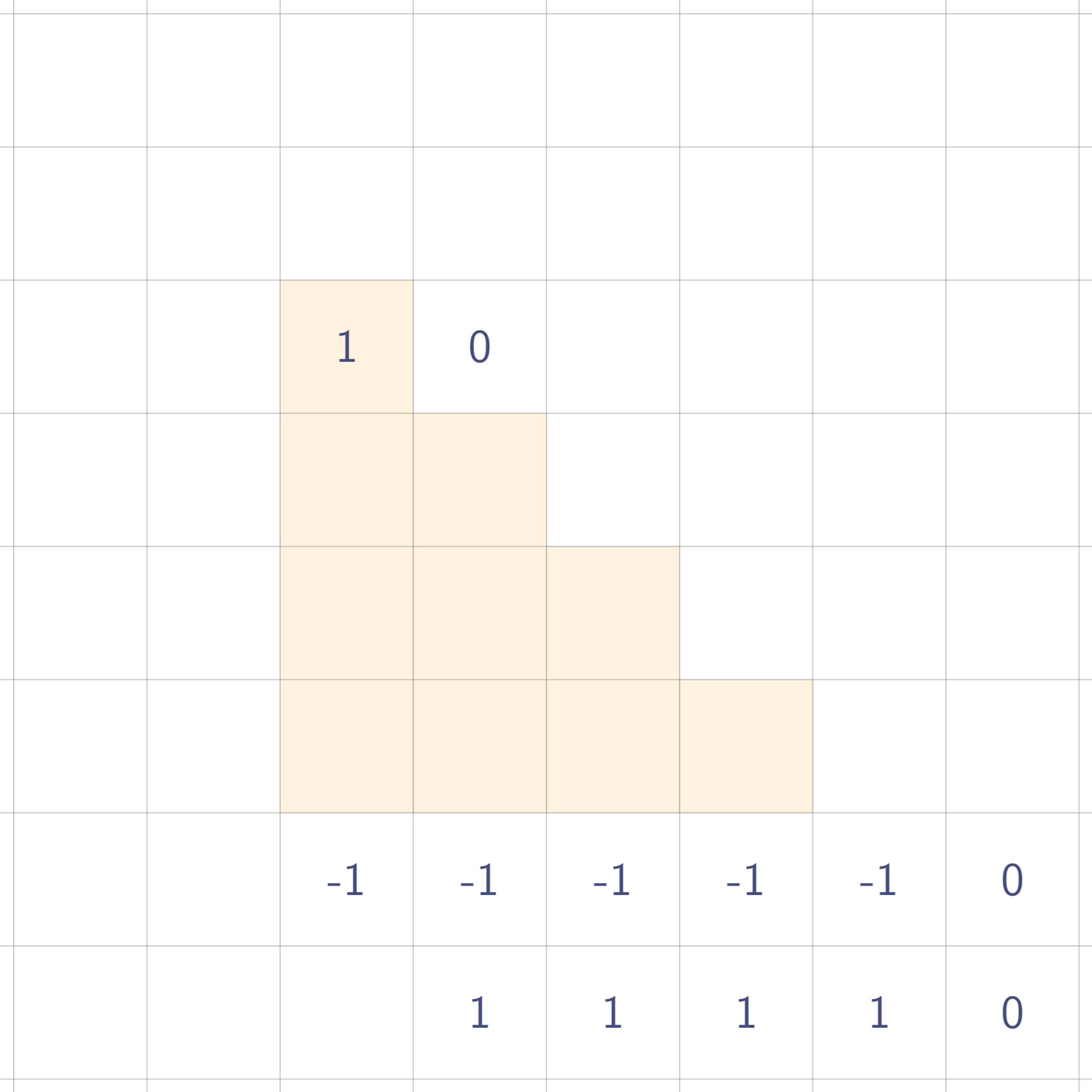
이제 휩쓴다는 게 무엇인지 감이 잡힐지도 모르겠다. 그냥 모든 행에 대해 왼쪽부터 누적합을 구하는 것이다. 세로 방향으로도 해 보자.
마찬가지로, 모든 열에 대해 위에서부터 누적합을 구하면 된다.
위에서 아까 봤던 이 사각형에도 적용할 수 있을까? 몇 번이고 말하지만, 각 사각형들에 대해 실제로 1을 모두 찍는 게 아니고, 값 4개만 제대로 찍어두고 나중에 두 번 휩쓸면 되는 것이다.
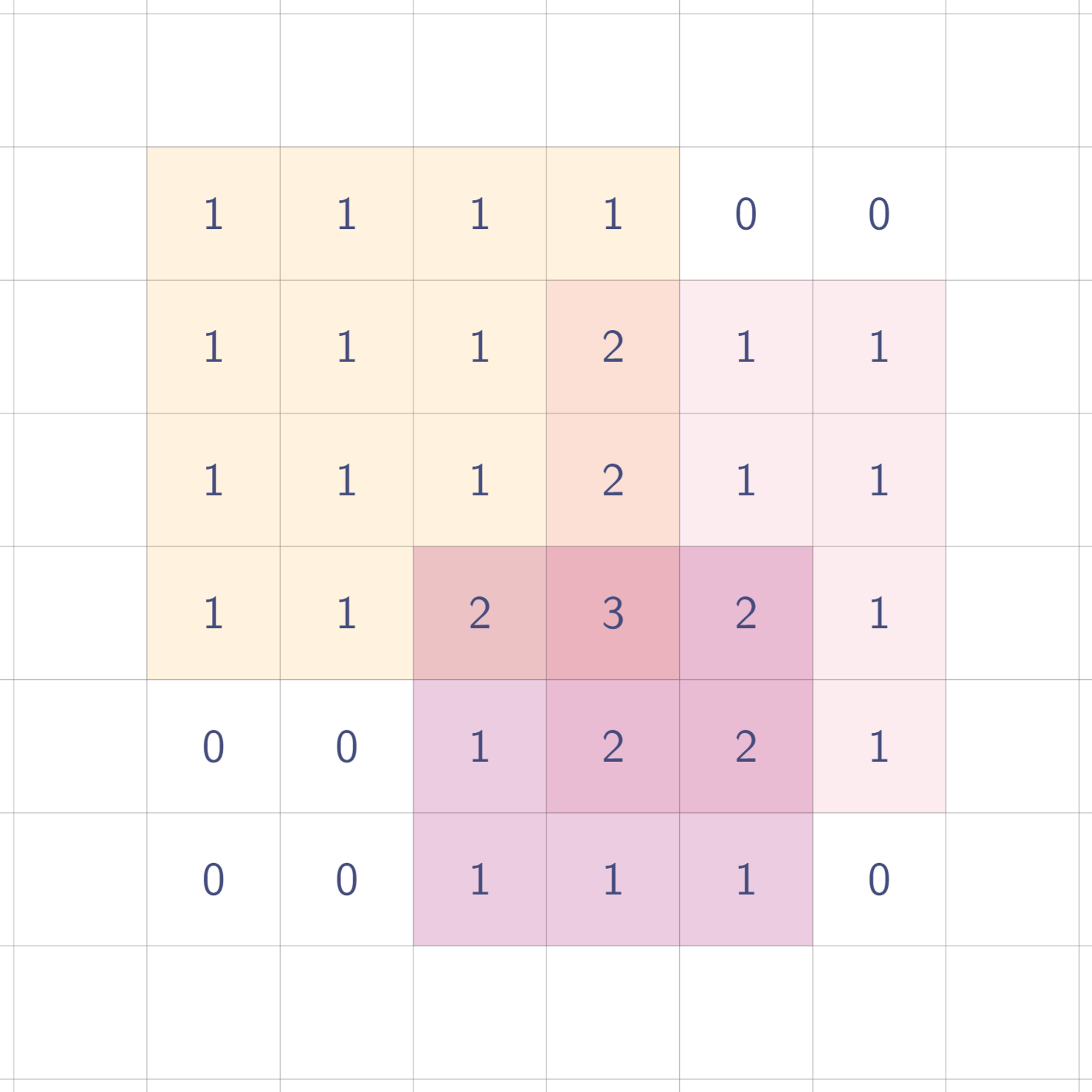
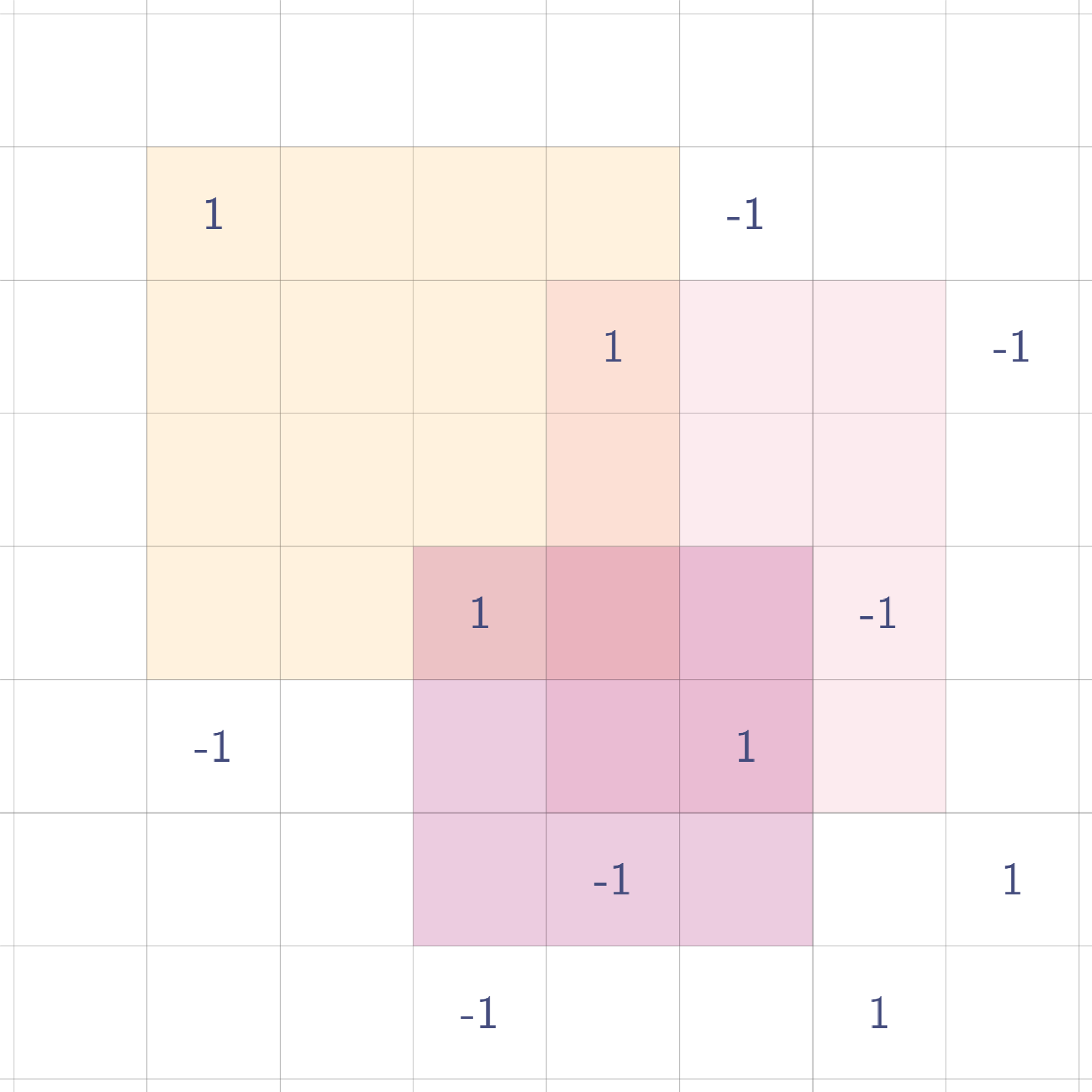
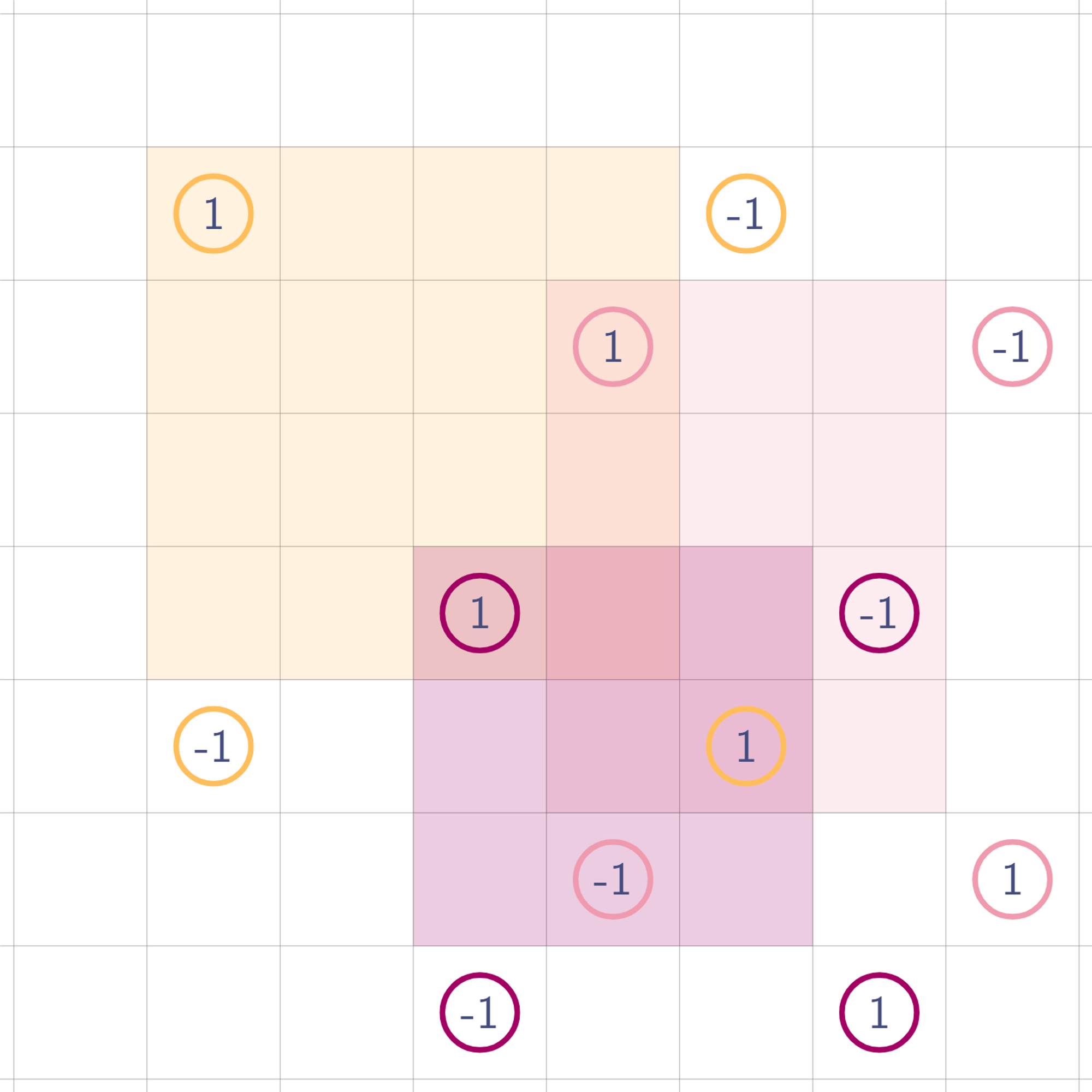
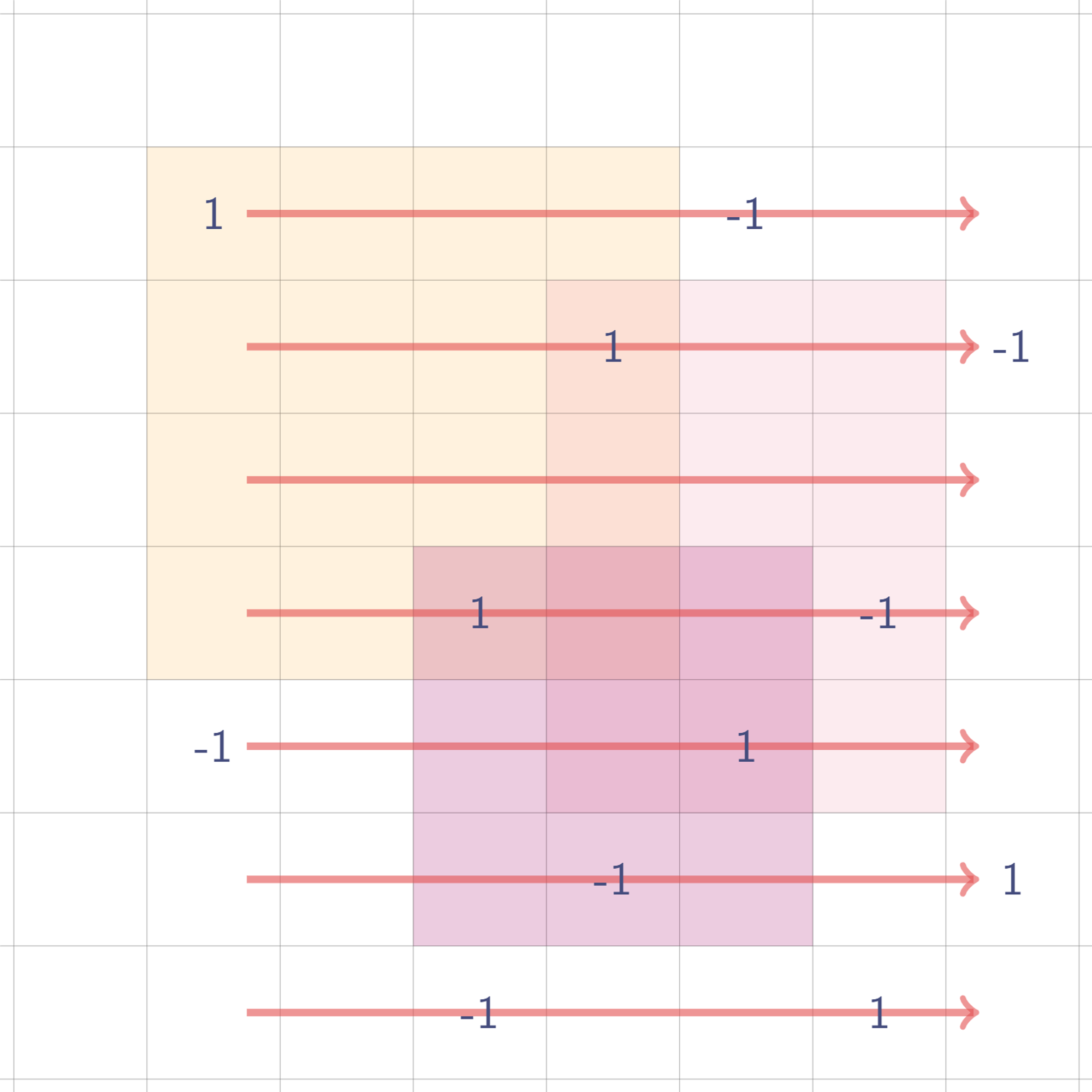
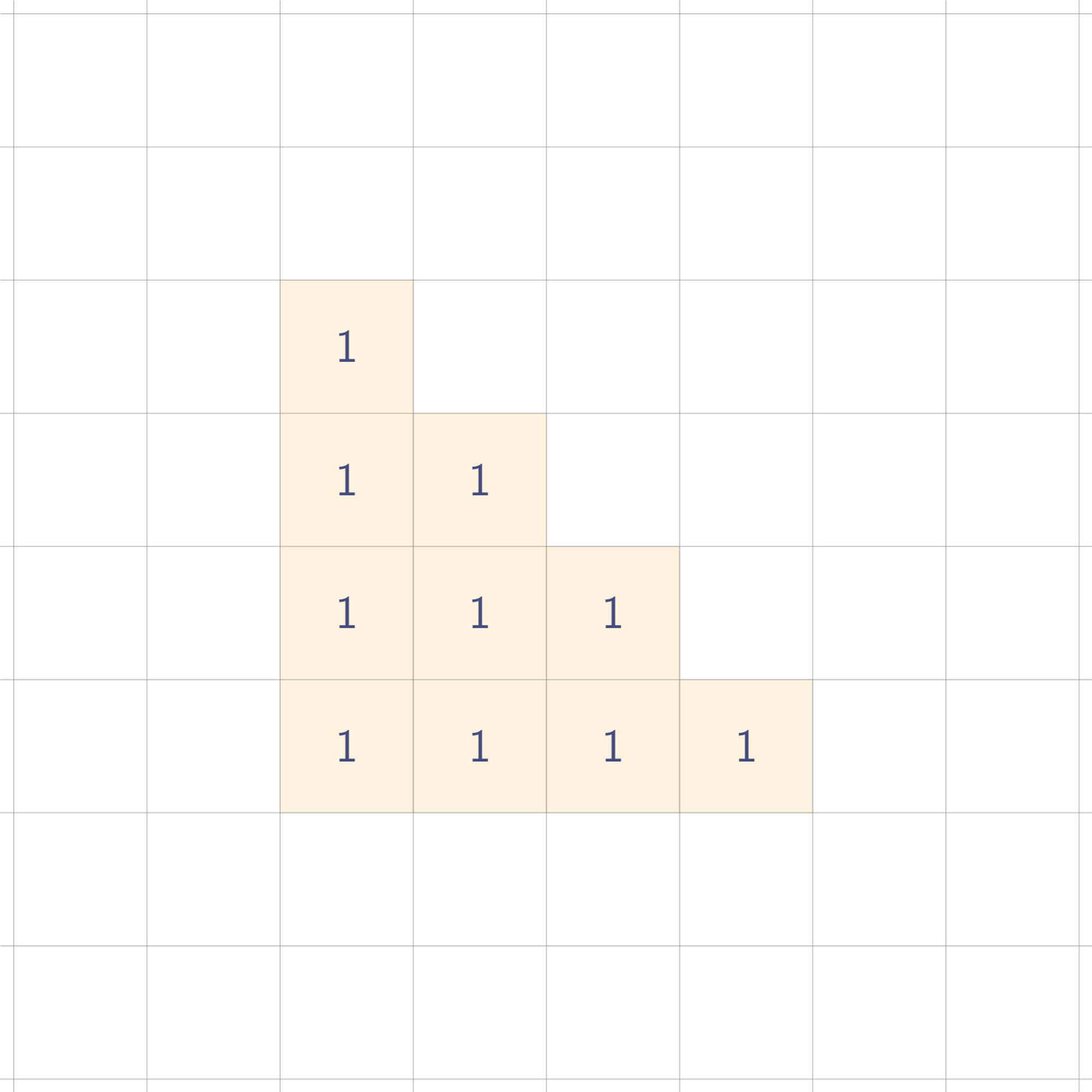
사각형 영역은 총 3개이다. 각 사각형들에 대해 값을 찍으면 이렇게 된다.
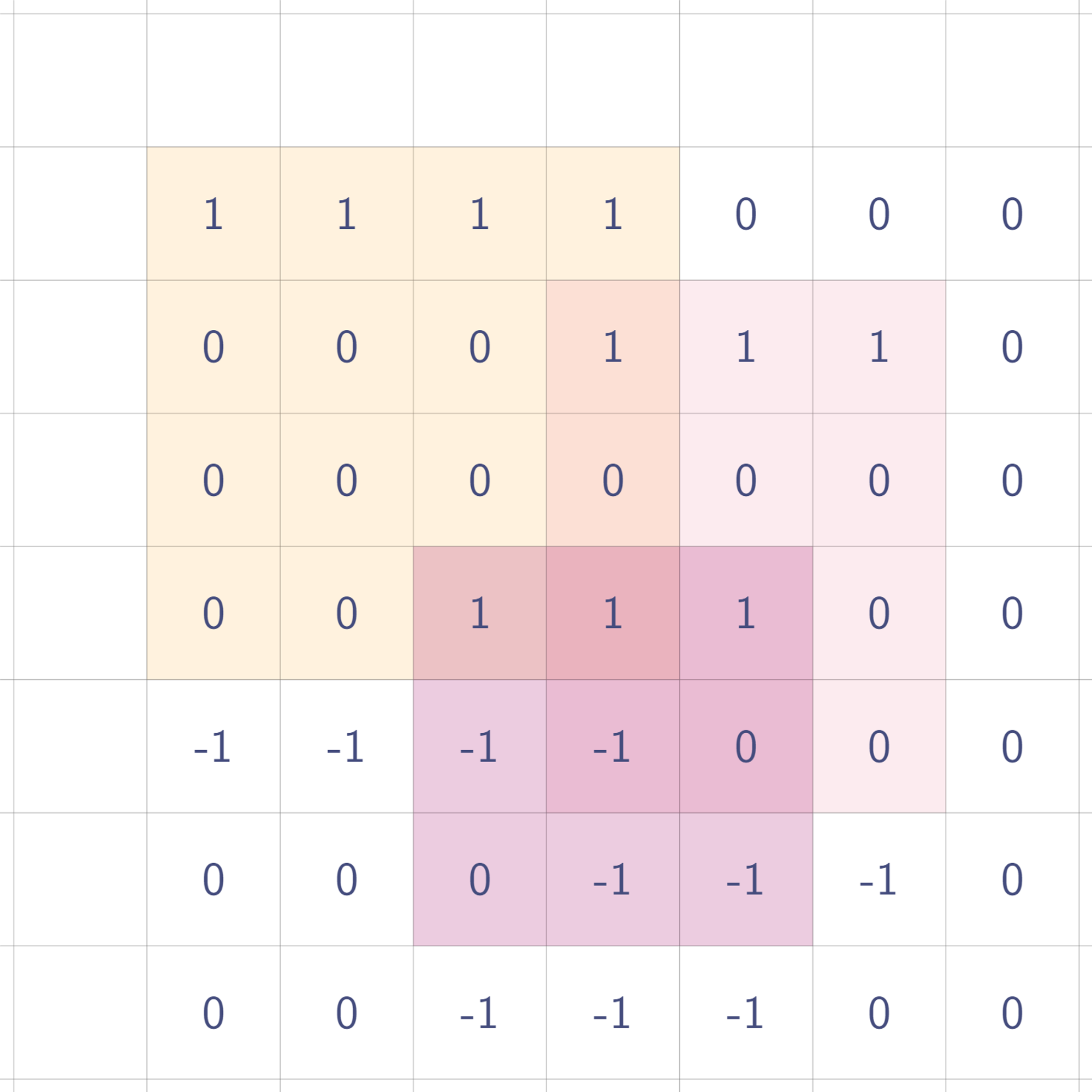
설명의 편의상, 각 사각형 영역이 관여하는 값에 같은 색으로 동그라미 표시하였다.
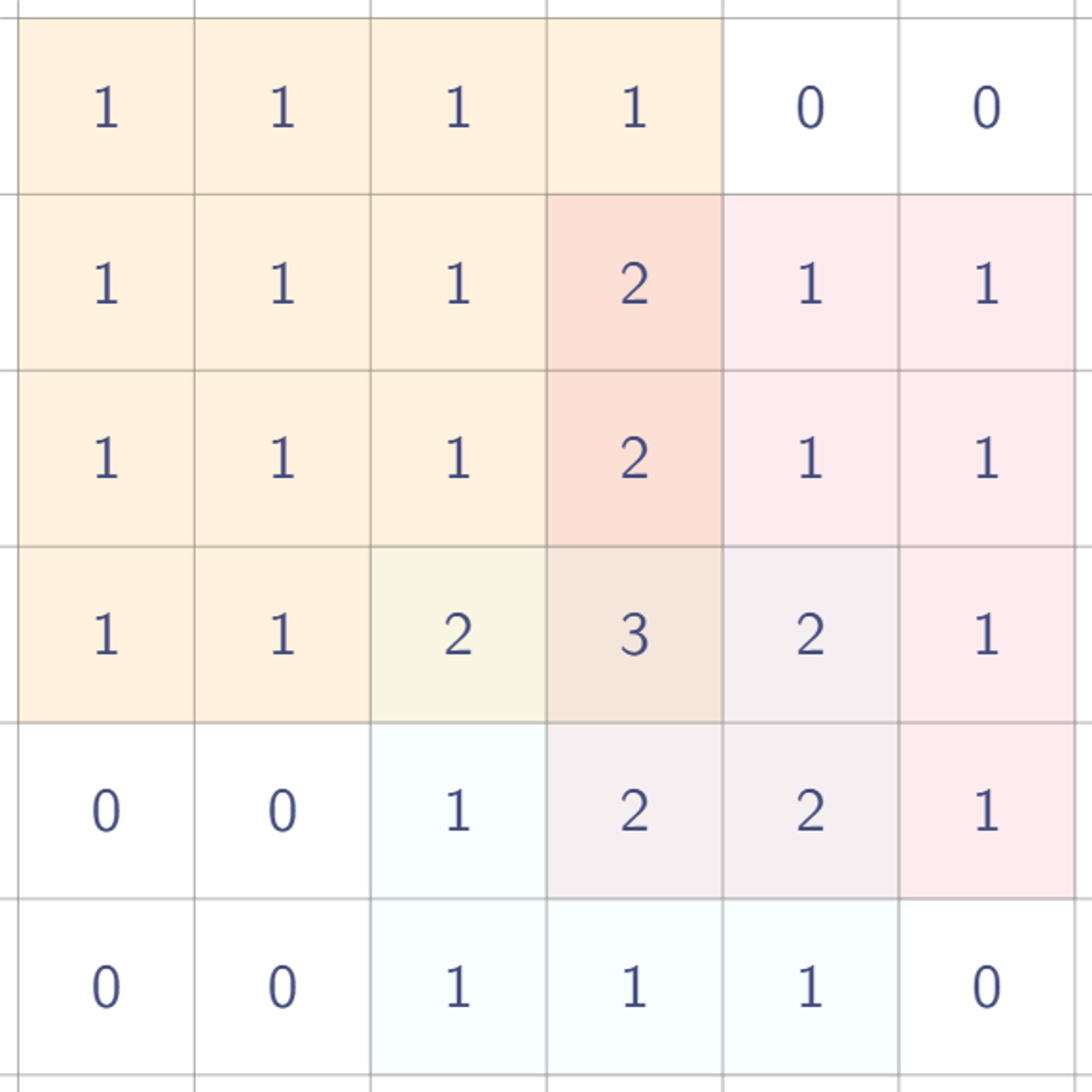
이제 이렇게 찍은 값들을 휩쓸어보자. 우선 오른쪽으로 한 번!
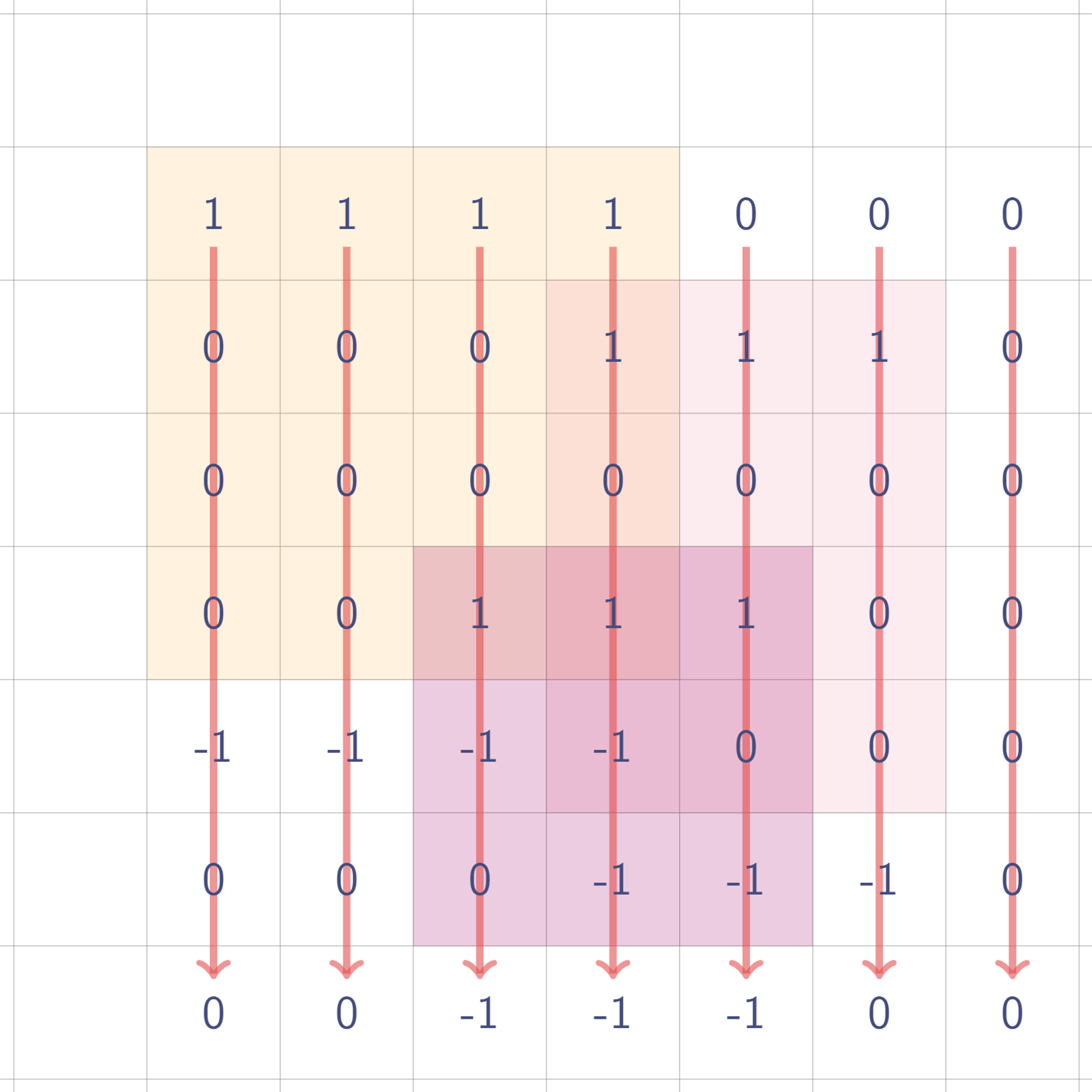
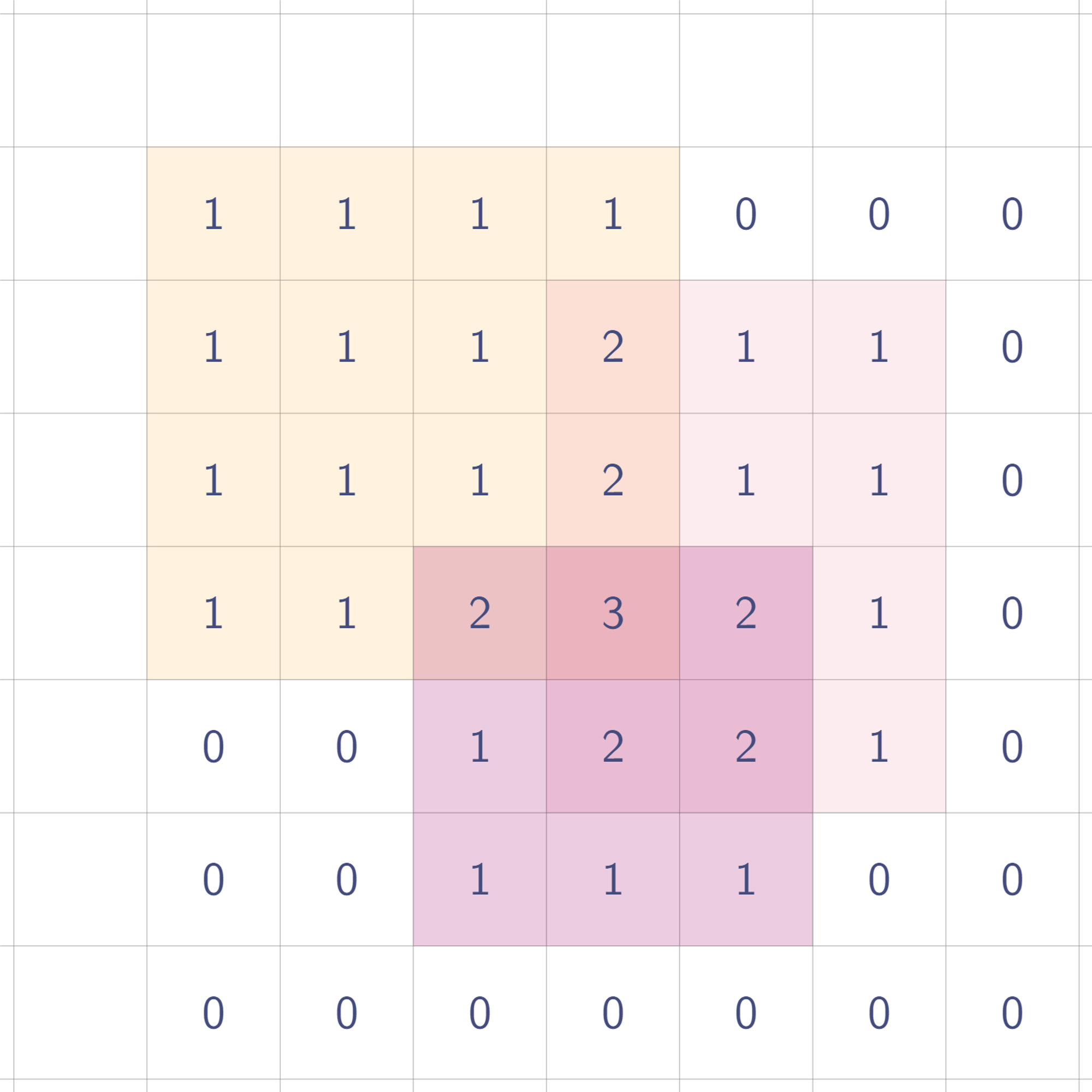
밑으로 한 번 휩쓸면?
짜잔! 원래 값을 복원할 수 있다!
특수 좌표계에서의 imos법
이 부분이 특히 재미있었고, 이 주제를 글로 쓰게 만든 이유이다. imos법은 그 특성상 다른 특수 좌표계에도 쉽게 적용이 가능하다.
특수 좌표계라고 하면 감이 잘 오지 않을 것이다. 정삼각형을 우선 예시로 들겠다.
삼각형에 imos법을 어떻게 적용할 수 있을까? 우선 삼각형은 2차원 배열에서 왼쪽 하단만 쓰는 식으로 쉽게 모델링할 수 있다. 몇 번이고 이야기하지만, imos법의 강력함은 영역을 '영역의 시작과 끝'으로만 일단 나타내고, 나중에 한번에 쓸어내면서 원래 값을 복원할 수 있다는 것이다.
삼각형 하나에 대해서 먼저 생각해보자.
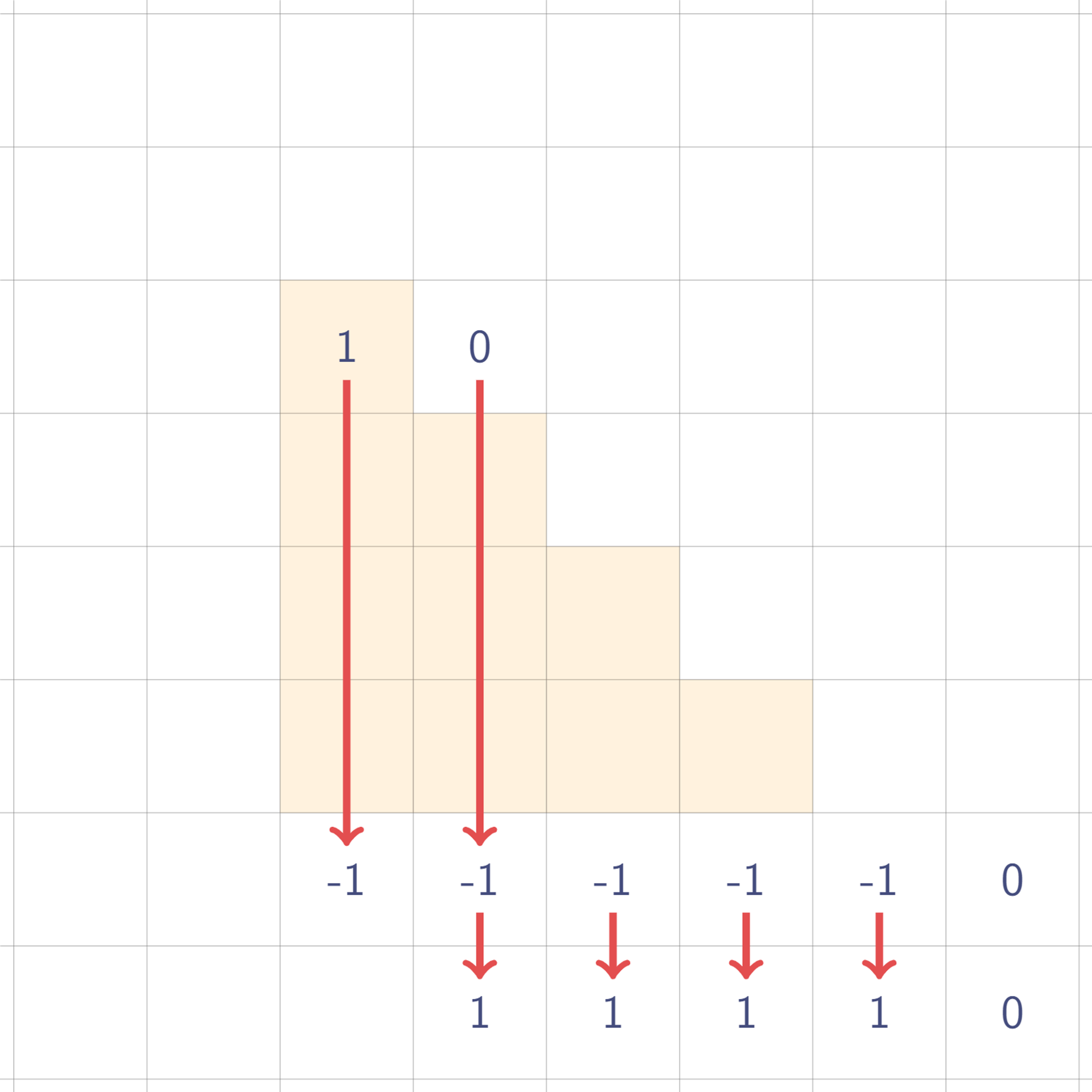
이렇게 생긴 삼각형도 사각형처럼 값만 딱 딱 찍어두고, 나중에 한 번에 복원할 수 있을까? 정답은 다음과 같다.
이렇게 찍어둔 뒤에 어떻게 하면 될까? 총 3번 휩쓸면 된다. 어렵지 않다!
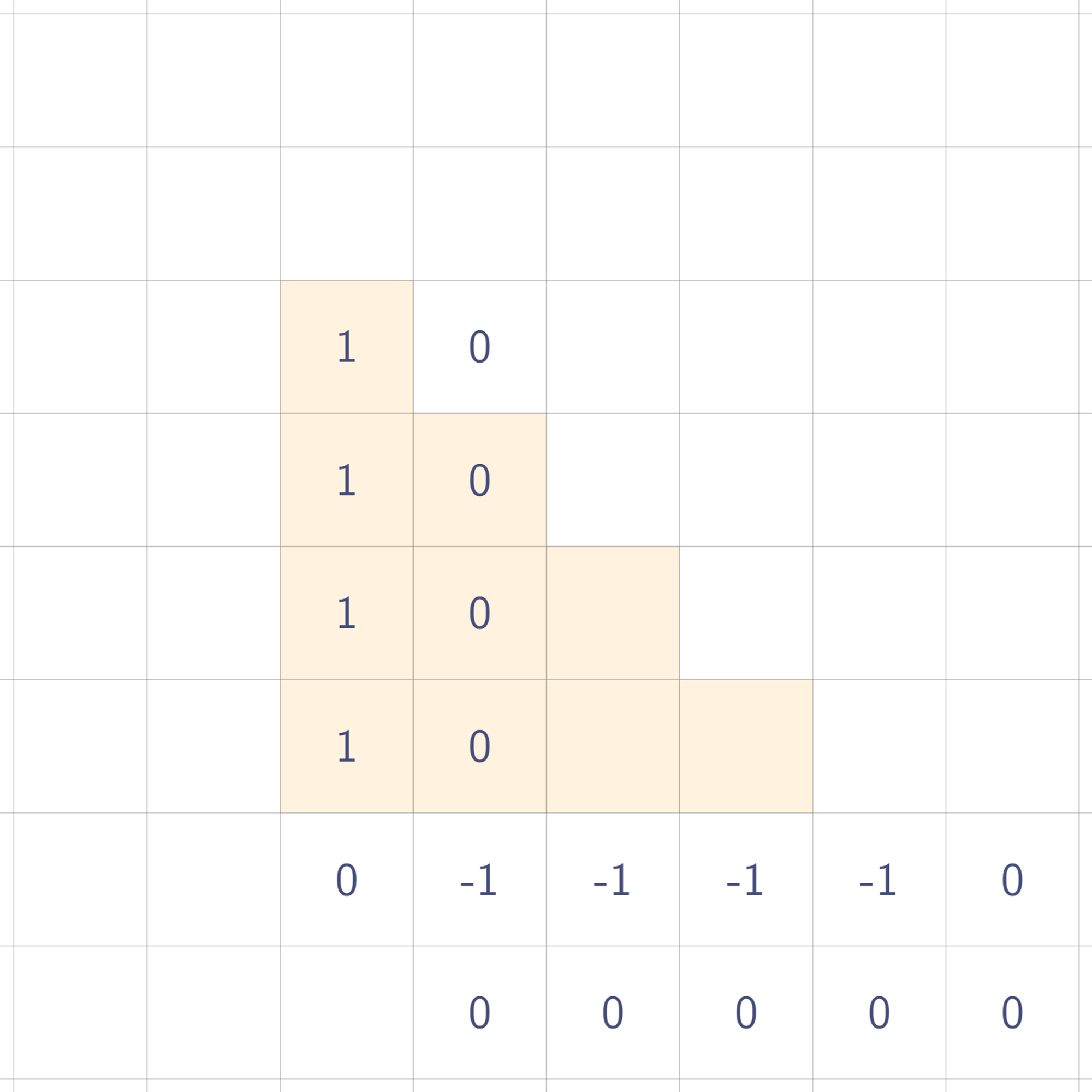
하나, 오른쪽으로 휩쓴다!
둘, 밑으로 휩쓴다!
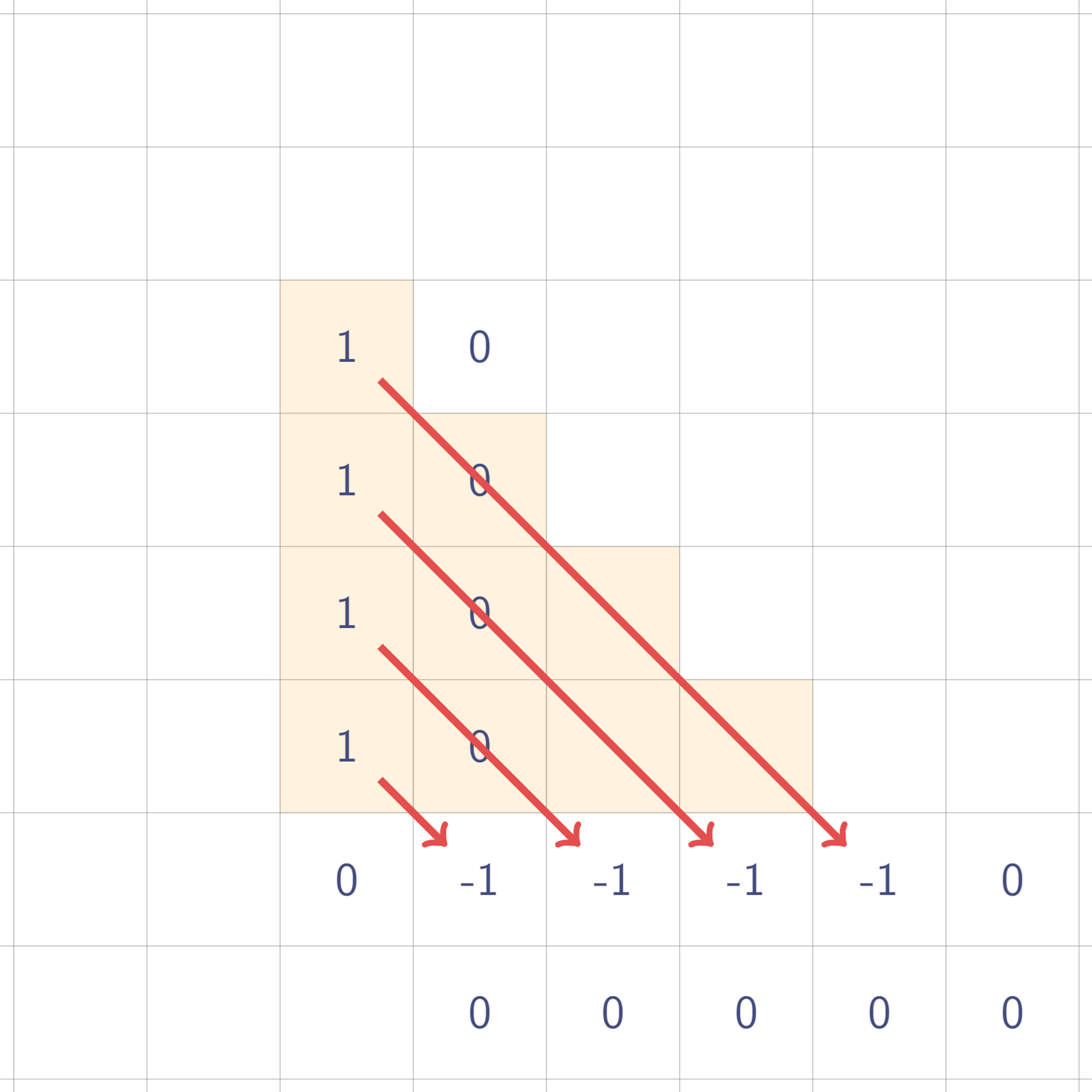
여기까지는 똑같다. 셋, 대각선으로 휩쓴다!
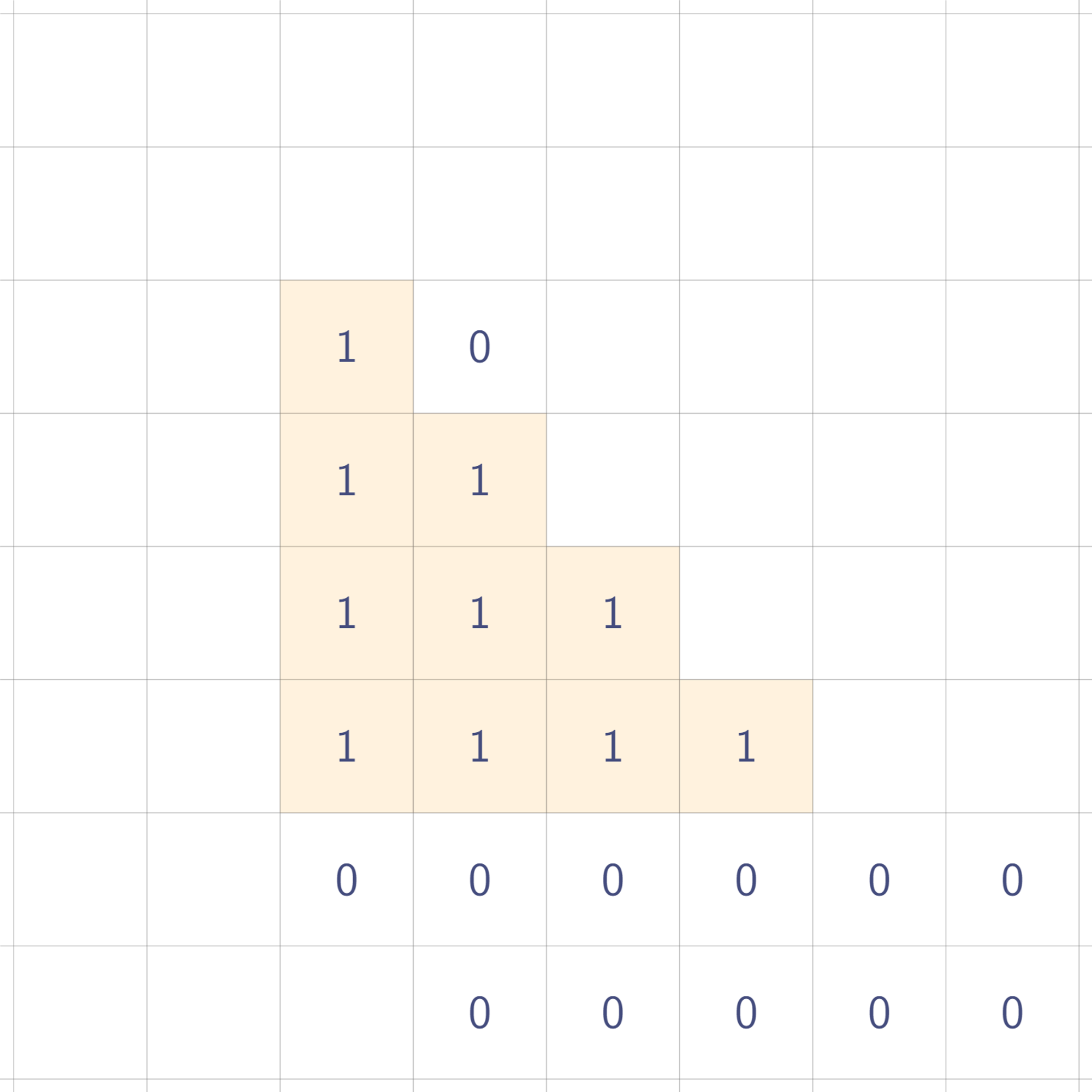
짠! 원래 삼각형이 복원되었다. 즉, 삼각형 모양도 값 여섯 개만 찍어두면 복원할 수 있는 것이다!
삼각형에 imos법을 적용하는 문제를 풀어보면서 바로 익혀보자.
BOJ::5541 - 釘
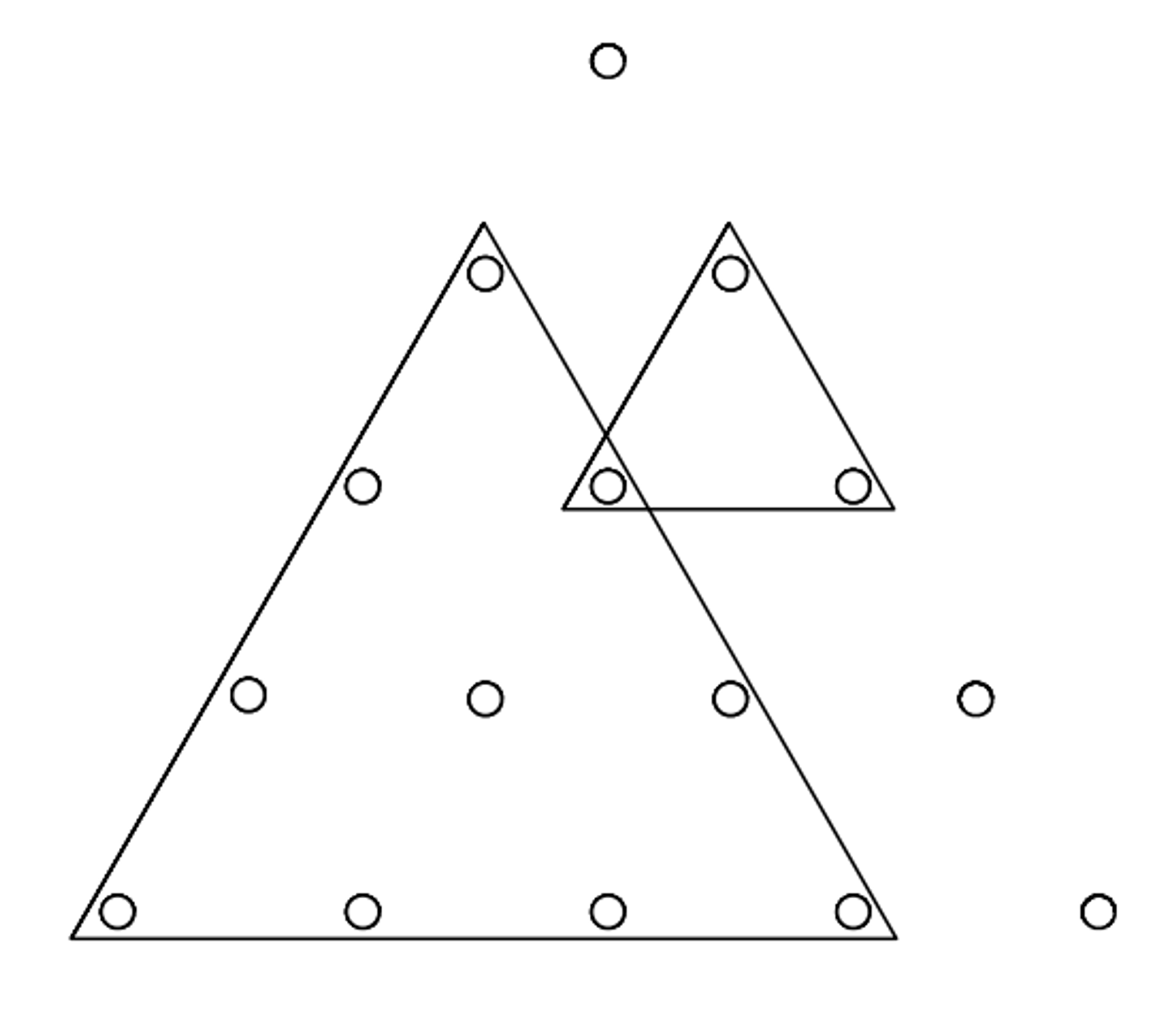
문제 자체는 일본어로 되어 있지만, 요약하자면 "정삼각형 판에 못이 박혀 있고 판에 정삼각형 모양으로 고무줄을 씌울 것인데, 최종적으로 고무줄이 씌워져 있는 못의 개수는?" 이 된다.
오른쪽과 같이 고무줄 두 개를 씌웠을 때, 고무줄이 씌워져 있는 못의 개수는 총 12개가 된다.
이 문제에 어떻게 imos법을 적용할 수 있을까? 간단하다. 고무줄 쿼리가 들어올 때마다 imos법으로 값을 찍어두고, 나중에 한 번에 휩쓸면서 시뮬레이팅한 뒤, 고무줄이 걸려 있는 영역(imos 배열이 1 이상인 영역)의 개수만 체크하면 된다.
코드는 다음과 같다.
정답 코드
BOJ::16436 - 얼룩말 아트
얘도 imos법을 써먹을 수 있는 문제이다. 풀이는 나중에 생각나면 적을게요 헤헤
정답 코드
imos법은 이외에도 육각형 좌표계 등 다양한 특수 좌표계에 써먹을 수 있다.